wxMaxima
[1] アニメ
(2019/06 半ば)
wxMaximaでアニメが作れると知ってトライ。参考サイトは http://nonoishi.web.fc2.com/maxima/Maxima-anim.html
俺んちの環境 Win 10 Pro(1809) DELL OPTIPLEX 7010SFF(Core-i5, 3.2GHz, 8GB Mem) + wxMaxima 18.10.1
正弦波の自己相関ってもののアニメ化。正弦波と位相をずらしつつ乗算する。sin(x)・sin(x - θ) の波形を見る。
sin(x), sin(x -θ), sin(x)・sin(x - θ) に加えて乗算結果の周期積分結果を表示する。
with_slider_draw(
k,makelist(i,i,-30,30)/10,
proportional_axes = xy,
xrange = [-10, 10],
yrange = [-4 , 4],
xaxis=true,
yaxis=true,
grid = true,
title = "Circle and
Line" ,
explicit(sin(x), x, -10, 10 ),
explicit(sin(x - k), x,
-10, 10 ),
color = red,
explicit(sin(x)*sin(x - k), x, -10, 10
),
color = black,
explicit(integrate(sin(x)*sin(x - k), x, 0,
2*%pi), x, -10, 10 )
);
これをWin 10 Pro DELL OPTIPLEX 7010SFF(Core-i5, 3.2GHz, 8GB Mem)で実行すると意外と時間がかかるです。
青固定 sin(x), 動くのがsin(x -θ)、赤いのが2つの乗算、直線が周期積分
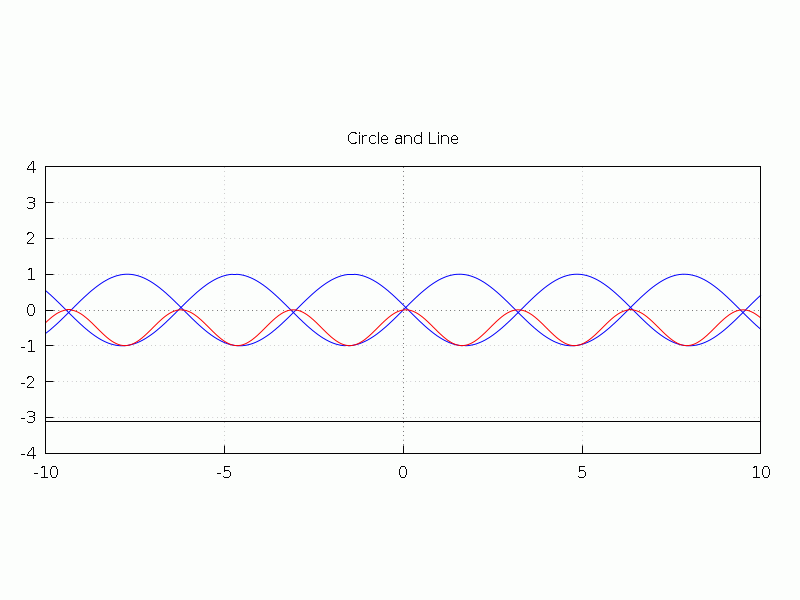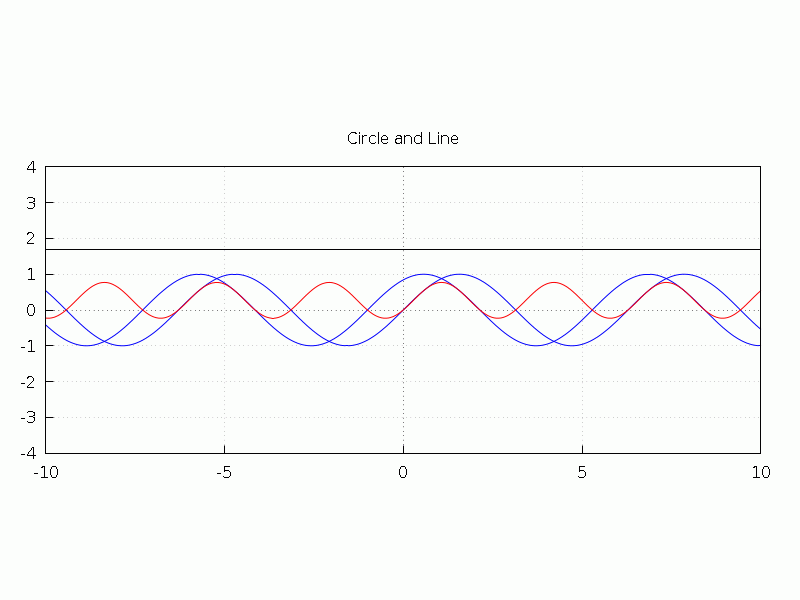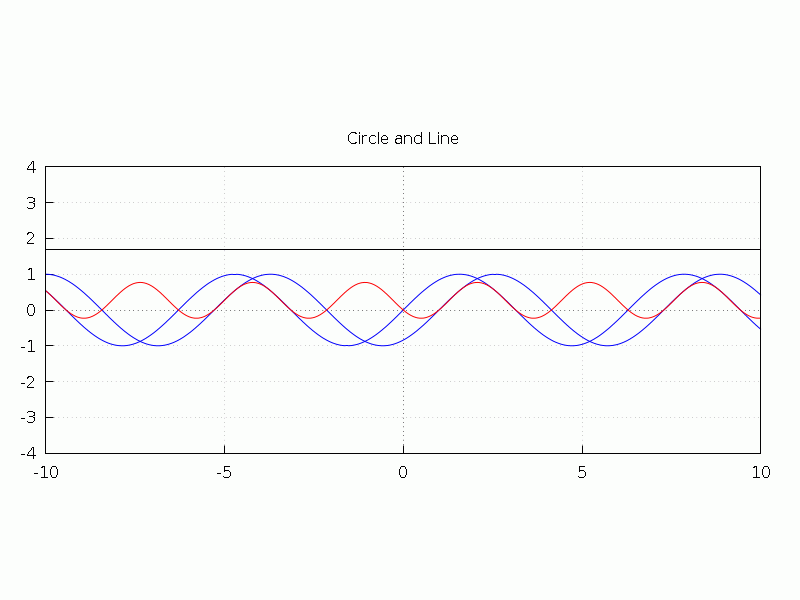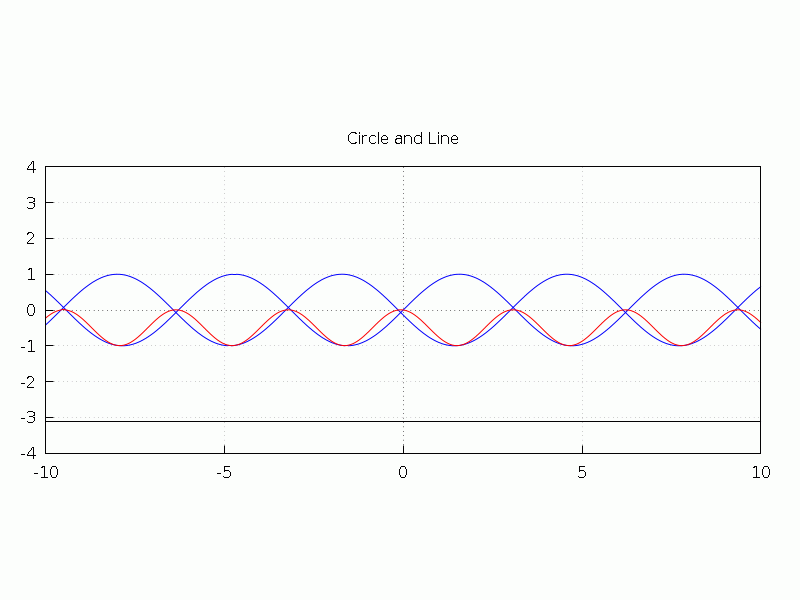
周期積分の計算
htmlのリンクだと一回別のタグ表示になるのでよくないな。画像を貼り付ける。
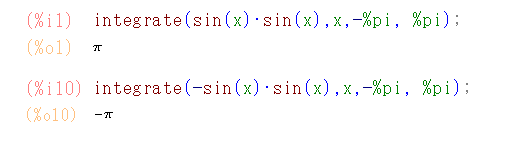
[2] 球面調和関数
(2019/06 半ば)
球面調和関数というものがある。量子力学・シュレディンガー方程式の解法で登場する。実は量子力学とは関係なく数学の分野のものなのだ。シュレディンガー方程式は2階線形微分方程式である。それをデカルト座標から極座標に変換して解く。Maximaは球面調和関数を用意してある。計算はそれを使えばいい。3次元表示は・・・これも用意されている。結果の一つはこういうものである。
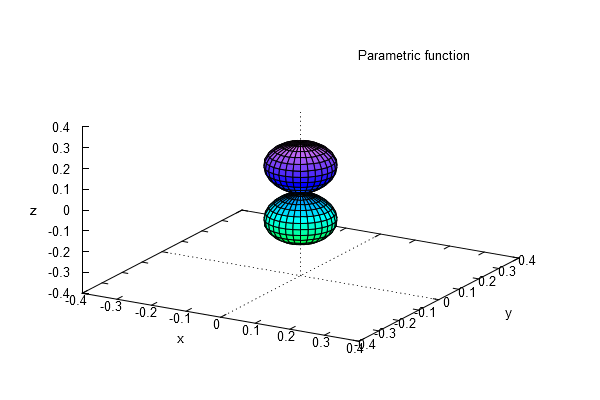
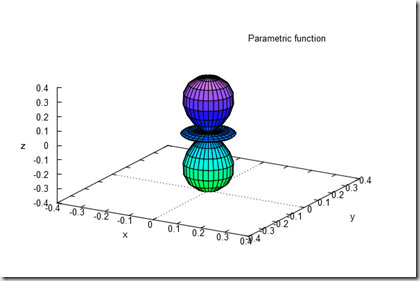

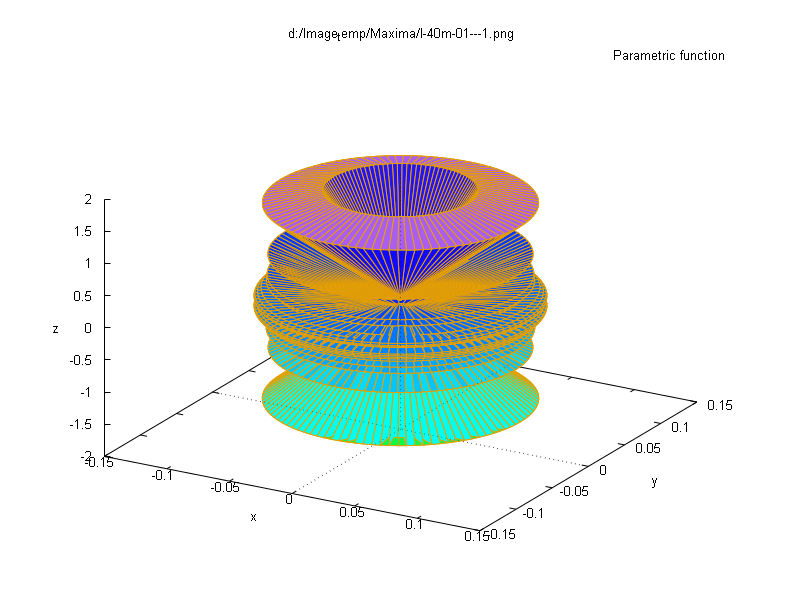
一応、能書きを垂れるとね。こういうの量子力学の解ではない。シュレディンガー方程式の解のうちの角度依存成分を表示しただけで解としては動径方向の成分もある。それを考慮した場合の3D表示はどうなるか。少しばかり表示が困難。。。というか、まったく困難。オレには表示は無理。上の図形は角度依存成分の値が同じである点を集めたものである。その内側ではどうなるか。その外側ではどうなるか。それは不明。単なる数式での話で面白い図形が出来る、という程度に見ておけばよい。
